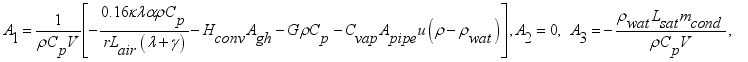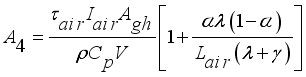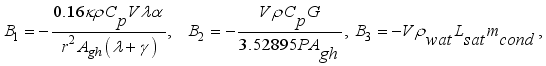1. Introduction
1.1. Background Information
In the last few decades, climate change has affected global agriculture and the Inter-Governmental Panel on Climate Change assessment report indicated that most countries have experienced increase in average temperature and periods of heavy precipitation. These climatic variability and changes have posed a threat to food production in areas where farming is predominantly rain-dependent and on small-scale for majority of the farmers. In order to counter the above mentioned challenges in Kenya, National Greenhouse Manufacturing Association proposed adaptation irrigation and greenhouse farming
| [12] | Edame, G. E., Ekpenyong, A., Fonta, W. M., & Duru, E. (2011). Climate change, food security and agricultural productivity in Africa: issues and policy directions. International journal of humanities and social science, 1(21), 205-223. |
| [19] | Kabubo-Mariara, J., & Kabara, M. Environment for Development. |
[12, 19]
. Greenhouse is a buildings used for the production of crops where more favorable climatical conditions are attained by applying the appropriate control methods. The greenhouses are built to gather light and to trap the considerable heat contained in sunshine
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [28] | Roy, J., Boulard, T., Kittas, C., & Wang, S. (2002). PA—Precision Agriculture: convective and ventilation transfers in greenhouses, Part 1: the greenhouse considered as a perfectly stirred tank. Biosystems Engineering, 83(1), 1-20. |
| [31] | Villarreal-Guerrero, F., Kacira, M., Fitz-Rodríguez, E., Linker, R., Kubota, C., Giacomelli, G. A., & Arbel, A. (2012). Simulated performance of a greenhouse cooling control strategy with natural ventilation and fog cooling. Biosystems Engineering, 111(2), 217-228. |
[7, 28, 31]
, as shown by
Figure 1. It is with this idea that the researchers of this paper used to improve the current and increase greenhouse farming in the Central Kenya. The ventilation of the greenhouse is required to remove heated air and introduce drier air for evaporative cooling. In areas with extremely high temperatures and very dry air, it may be possible to maintain cooler air temperatures than outdoors by taking advantage of the combined effects of evaporative cooling equipment and crop transpiration
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [8] | Chao, J., Knickerbocker, R., North, P., Swift, D., Long, A., & Shtylla, B. (2014). Simple Model of Temperature in the Pomona College Organic Farm Greenhouse. |
| [11] | Dwyer, D. (2014). Defining ventilation boundary conditions for a greenhouse climate model. |
| [25] | Radojević, N., Kostadinović, D., Vlajković, H., & Veg, E. (2014). Microclimate control in greenhouses. FME Transactions, 42(2), 167-171. |
[7, 8, 11, 25]
.
Figure 1. Dimensions of the greenhouse under study.
In a greenhouse heat and mass transfer (HMT), mainly occur through convection which is the movement of groups of molecules within fluid either by diffusion or by advection; heat fluxes are due to condensation of water vapor, from solar radiation, ventilation, and plant transpiration. Most of convective heat fluxes exchanging between different parts of the greenhouse depend on the heat transfer coefficients and the temperature difference between the elements surface and the air. Water vapor content of the air inside the greenhouse is an important environmental parameter, which determines the proper development of a crop. The model describing the changes in the water vapor content of the air inside the greenhouse is based on the mass balance equation. Mass transfer due to ventilation can take place in both directions depending on the conditions inside and outside the greenhouse
| [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [8] | Chao, J., Knickerbocker, R., North, P., Swift, D., Long, A., & Shtylla, B. (2014). Simple Model of Temperature in the Pomona College Organic Farm Greenhouse. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
[5, 6, 8, 10]
.
When the modeling had been done, the governing equations were solved to obtain the required solution. In the study, dynamic model was used to express behavior of the system over time where a model of a system is the replica of the system, which had all the properties and functions of the system, and simulation was the process by which computer was used to reproduce the behavior of a system using a model. Simulation of a system was represented as the running of the system's model which was used to explore and gain new insights into new technology besides estimating the performance of systems that are too complex for analytical solutions. In the analysis, assumptions were made to simplify the model divided it into number of sub-models as shown by
Figure 2, where each sub-model was treated independently before they were integrated together. Often dynamic systems required control system to perform properly thus, PID controller was designed to attain the study objectives
| [3] | Ali, R. B., Aridhi, E., & Mami, A. (2015). Dynamic model of an agricultural greenhouse using Matlab-Simulink environment. Paper presented at the Sciences and Techniques of Automatic Control and Computer Engineering (STA), 2015 16th International Conference on. |
| [9] | Chaturvedi, D. K. (2009). Modeling and simulation of systems using MATLAB and Simulink: CRC Press. |
| [14] | Fahmy, F. H., Farghally, H. M., Ahmed, N. M., & Nafeh, A. (2012). Modeling and simulation of evaporative cooling system in controlled environment greenhouse. Smart Grid and Renewable Energy, 3(01), 67. |
| [17] | Goosse, H., Barriat, P., Lefebvre, W., Loutre, M., & Zunz, V. (2010). Introduction to climate dynamics and climate modeling. Online textbook. In. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[3, 9, 14, 17, 27]
.
Figure 2. Schematic representation of the Modeling process.
Mathematical modeling can either be black-box model or white-box model depending with available information. In black-box models estimate both the functional relationship between variables and the numerical parameters in those functions and artificial neural networks approach is usually applied, which usually does not need anything except the input and output data sets. These models are mainly used for complex systems, especially when input-output patterns are in quantitative form and when they not in quantitative form, fuzzy models are used, as shown by
Figure 3 shows the relationship between inputs and outputs of a system
| [2] | Alghannam, A. R. O. (2012). Using proportional integral derivative and Fuzzy logic with optimization for greenhouse. International Journal of Latest Trends in Agriculture and Food Sciences, 2(2). |
| [15] | Faouzi, D., & Bibi-Triki, N. (2016). Modeling, Simulation and Optimization of agricultural greenhouse microclimate by the application of artificial intelligence and/or fuzzy logic. |
| [17] | Goosse, H., Barriat, P., Lefebvre, W., Loutre, M., & Zunz, V. (2010). Introduction to climate dynamics and climate modeling. Online textbook. In. |
| [26] | Rodríguez, F., Berenguel, M., Guzmán, J. L., & Ramírez-Arias, A. (2015). Modeling and control of greenhouse crop growth: Springer. |
| [29] | Sriraman, A., & Mayorga, R. (2007). Climate Control inside a Greenhouse: An Intelligence System Approach Using Fuzzy Logic Programming. Journal of Environmental Informatics, 10(2). |
| [30] | Velten, K. (2009). Mathematical modeling and simulation: introduction for scientists and engineers: John Wiley & Sons. |
[2, 15, 17, 26, 29, 30]
.
Figure 3. Representation of Mathematical Model.
1.2. Statement of Research Problem
Most of famers practicing greenhouse farming control the temperature and humidity by conventional methods of opening and closing the greenhouses walls. This method affects the yields as the temperature and humidity level required by different plants for maximum production are not guaranteed. This is the concept that formed the base of the research to formulate auto-tuned MATLAB-SIMULINK model of convective HMT inside a greenhouse and use the results to improve the cooling and ventilating systems. Analysis of simulation results allowed to make statement of logical correctness of the developed model and makes it possible to determine.
1.3. Objectives of the Study
The study was done with objective of performing three-dimensional MATLAB-SIMULINK dynamic model for convective HMT for ventilating systems inside a greenhouse, and then:
1. Determine the modes of convection heat and mass transfer (CHMT) of the gases and vapour inside the greenhouse and,
2. Develop an auto-tuned PID-controlled dynamic mathematical MATLAB-SIMULINK model of CHMT exchange of the air inside a greenhouse, where growing of different crops could be carried out.
1.4. Assumptions Made
During the formulation of the mathematical model for these processes, equations of heat and mass balances for the air inside the greenhouse were developed aided by
| [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
[5, 6, 10, 24]
with the following simplifying assumptions:
1. The flow of the gases and vapor inside the greenhouse was assumed to be incompressible and lamina,
2. In the system, effect of energy loses was neglected,
3. Impact of the ground on the HMT was neglected,
4. The evaporation from the greenhouse cover and crops was neglected, because in modern greenhouses the condensate is drained from the cover.
2. Literature Review
2.1. Introduction
The dynamic behavior of the micro-climate inside a greenhouse is a combination of physical processes involving energy transfer and mass balance. The internal processes depend on the outside environmental conditions, structure of the greenhouse, type and state of the crop, and on the effect of the control actuators. The development of models of a dynamic system is a complex process that depends on the characteristics of the dynamics of the process object of study as guided by
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [15] | Faouzi, D., & Bibi-Triki, N. (2016). Modeling, Simulation and Optimization of agricultural greenhouse microclimate by the application of artificial intelligence and/or fuzzy logic. |
| [17] | Goosse, H., Barriat, P., Lefebvre, W., Loutre, M., & Zunz, V. (2010). Introduction to climate dynamics and climate modeling. Online textbook. In. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[7, 15, 17, 27]
. These models have been developed in different parts of the world and applied to several greenhouse structures under different climatic actuators, cover materials and crops. Although all these models are based on the same physical principles, they showed differences in the approaches used when adapted to the particular conditions in each area. All these works describe the basic equations of the mathematical models and include some results, but they do not describe the complete methodology used for the implementation, calibration, and validation of the models. To model the climate that is generated inside a greenhouse based on physical, physiological, biological, and chemical principles, mass and energy balances have to be applied to all its constitutive elements. The internal greenhouse climate is a function of air temperature, water content in the air, external temperatures, surface of the cover, crop type and soil characteristic. Besides the climatical variables, in modeling greenhouse climate one has to consider the presence or absence of installed actuators that constitute the inputs to the system and that can be artificially manipulated. In models of the greenhouse, principle of continuity between its elements applies, so that the HMT processes in each can be studied using mass and energy equations
| [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
[5-7, 10]
.
2.2. Literature Review
A number of researchers have in the last two decades performed modeling of the greenhouses climate and applied MATLAB-SIMULINK in their models. Agricultural greenhouse aims to create a favorable micro-climate to the requirements of growth and development of culture, from the surrounding weather conditions, produce according to the cropping calendars fruits, vegetables and flower species out of season and widely available along the year. It is defined by its structural and functional architecture, the quality thermal, mechanical and optical of its wall, with its sealing level and the technical and technological accompanying. The greenhouse is a very confined environment, where multiple components are exchanged between key stakeholders and those factors are light, temperature and relative humidity
| [3] | Ali, R. B., Aridhi, E., & Mami, A. (2015). Dynamic model of an agricultural greenhouse using Matlab-Simulink environment. Paper presented at the Sciences and Techniques of Automatic Control and Computer Engineering (STA), 2015 16th International Conference on. |
| [9] | Chaturvedi, D. K. (2009). Modeling and simulation of systems using MATLAB and Simulink: CRC Press. |
| [20] | Karris, S. T. (2006). Introduction to Simulink with engineering applications: Orchard Publications. |
| [21] | Leite, E. P. (2010). Matlab: modelling, programming and simulations: Sciyo. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [28] | Roy, J., Boulard, T., Kittas, C., & Wang, S. (2002). PA—Precision Agriculture: convective and ventilation transfers in greenhouses, Part 1: the greenhouse considered as a perfectly stirred tank. Biosystems Engineering, 83(1), 1-20. |
[3, 9, 20, 21, 24, 28]
. Thus, development of applicable cooling technologies is an important research endeavor. And appropriate greenhouse design, right choice of cladding material coupled with suitable ventilation and cooling techniques address the problems of summer greenhouse production of high temperature regions. So, there is a necessity to carry out in deep investigation on the design aspects of greenhouse and its functional characteristics influence on micro-climate. This information is useful for the researchers’ work on the engineering aspects of greenhouse technology
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [8] | Chao, J., Knickerbocker, R., North, P., Swift, D., Long, A., & Shtylla, B. (2014). Simple Model of Temperature in the Pomona College Organic Farm Greenhouse. |
| [17] | Goosse, H., Barriat, P., Lefebvre, W., Loutre, M., & Zunz, V. (2010). Introduction to climate dynamics and climate modeling. Online textbook. In. |
| [21] | Leite, E. P. (2010). Matlab: modelling, programming and simulations: Sciyo. |
| [25] | Radojević, N., Kostadinović, D., Vlajković, H., & Veg, E. (2014). Microclimate control in greenhouses. FME Transactions, 42(2), 167-171. |
[7, 8, 17, 21, 25]
, that is:
1. Adaptation of literature models to the test object, by taking into account characteristic dimensions of the tested greenhouse and its technical equipment,
2. Solve the governing equations for convective HMT inside the greenhouse.
3. Draw up a computer model and perform simulations, and,
4. Graphical and statistical validation of the resulting model of the process of heat exchange and mass transfer in the air inside the greenhouse using the results of experimental studies.
2.3. Greenhouses Technology
Figure 4. Some samples of greenhouses found in Kenya.
In some of the temperate regions where the climatic conditions are extremely adverse, no crops can be grown but man has developed methods of growing some high value crop continuously by providing protection from the excessive cold, which is called as greenhouse technology: technique of providing favorable environment condition to the plants. It is rather used to protect the plants from the adverse climatic conditions such as wind, cold, precipitation, excessive radiation, extreme temperature, insects and diseases. It is also important to create an ideal microclimate around the plants which is possible by erecting a greenhouse, where the environmental conditions are so modified that one can grow any plant in any place at any time by providing suitable environmental conditions with minimum labor. Greenhouses are of different types in relation to use, cost, environmental and geographical location and the material used to cover them. Although there are advantages in each type for a particular application, in general there is no single type greenhouse, which can be constituted as the best, and shown by
Figure 4(a) to (f) | [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [8] | Chao, J., Knickerbocker, R., North, P., Swift, D., Long, A., & Shtylla, B. (2014). Simple Model of Temperature in the Pomona College Organic Farm Greenhouse. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [28] | Roy, J., Boulard, T., Kittas, C., & Wang, S. (2002). PA—Precision Agriculture: convective and ventilation transfers in greenhouses, Part 1: the greenhouse considered as a perfectly stirred tank. Biosystems Engineering, 83(1), 1-20. |
| [31] | Villarreal-Guerrero, F., Kacira, M., Fitz-Rodríguez, E., Linker, R., Kubota, C., Giacomelli, G. A., & Arbel, A. (2012). Simulated performance of a greenhouse cooling control strategy with natural ventilation and fog cooling. Biosystems Engineering, 111(2), 217-228. |
[6-8, 24, 28, 31]
.
2.4. Factor Affecting Greenhouse Environment
The dynamic behavior of the greenhouse microclimate is a combination of physical processes involving energy transfer and mass balance. Temperature is the most important variable of the greenhouse climate that can and needs to be controlled. The majority of the crops grown in greenhouses is warm-season species which are adapted to average temperatures in the range 17°C and 27°C. For optimum production, air humidity is another important variable, which has traditionally been expressed in terms of relative humidity. Relative humidity within the range 60 and 90% is suitable to plant growth. Values below 60% may occur during ventila tion in arid climates, or when plants are young with small leaves, and this can cause water stress. Serious problems can occur if the relative humidity exceeds 95% for long periods, and favor rapid development of fungal diseases.
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [8] | Chao, J., Knickerbocker, R., North, P., Swift, D., Long, A., & Shtylla, B. (2014). Simple Model of Temperature in the Pomona College Organic Farm Greenhouse. |
| [11] | Dwyer, D. (2014). Defining ventilation boundary conditions for a greenhouse climate model. |
| [14] | Fahmy, F. H., Farghally, H. M., Ahmed, N. M., & Nafeh, A. (2012). Modeling and simulation of evaporative cooling system in controlled environment greenhouse. Smart Grid and Renewable Energy, 3(01), 67. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [28] | Roy, J., Boulard, T., Kittas, C., & Wang, S. (2002). PA—Precision Agriculture: convective and ventilation transfers in greenhouses, Part 1: the greenhouse considered as a perfectly stirred tank. Biosystems Engineering, 83(1), 1-20. |
[7, 8, 11, 14, 24, 28]
.
2.5. Energy and Mass Balances
Convective heat transfer is transfer of heat from one place to another via movement of fluids. Practically, convective heat transfer involves the combined processes of unknown conduction and advection. This motion is associated with large numbers of molecules are moving collectively or as aggregates. Such motion, in the presence of a temperature gradient, contributes to heat transfer. Because the molecules in aggregate retain their random motion, the total heat transfer is then due to the superposition of energy transport by random motion of the molecules and by the bulk motion of the fluid, shown in
Figure 5 | [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[5, 6, 10, 27].
Mass transfer between a moving fluid and a surface or between immiscible moving fluids separated by a mobile interface is often aided by the dynamic characteristics of the moving fluid. This mode of transfer is called convective mass transfer, with the transfer always going from a higher to a lower concentration of the species being transferred. Convective transfer depends on both the transport properties and the dynamic characteristics of the flowing fluid. When an external pump or similar device causes the fluid motion, the process is called forced convection. If the fluid motion is due to a density difference, the process is called free or natural convection shown in
Figure 5 | [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[5, 6, 10, 27]
.
Figure 5. Modes of heat and mass exchange inside and outside a greenhouse.
2.6. Structural Requirements
The National Greenhouse Manufacturing Association developed excellent standards for ventilating and cooling greenhouses. These include recommendations and designs affecting site elevation, sunlight intensity, orientation and shape of the greenhouse and crops being grown
| [14] | Fahmy, F. H., Farghally, H. M., Ahmed, N. M., & Nafeh, A. (2012). Modeling and simulation of evaporative cooling system in controlled environment greenhouse. Smart Grid and Renewable Energy, 3(01), 67. |
| [31] | Villarreal-Guerrero, F., Kacira, M., Fitz-Rodríguez, E., Linker, R., Kubota, C., Giacomelli, G. A., & Arbel, A. (2012). Simulated performance of a greenhouse cooling control strategy with natural ventilation and fog cooling. Biosystems Engineering, 111(2), 217-228. |
[14, 31]
. The following is a discussion of systems and requirements. Greenhouse ventilation is required to regulate temperature and moisture levels and provide carbon dioxide for good crop production. There are two basic ventilation systems used in greenhouse production systems, natural and mechanical ventilation systems
| [11] | Dwyer, D. (2014). Defining ventilation boundary conditions for a greenhouse climate model. |
| [14] | Fahmy, F. H., Farghally, H. M., Ahmed, N. M., & Nafeh, A. (2012). Modeling and simulation of evaporative cooling system in controlled environment greenhouse. Smart Grid and Renewable Energy, 3(01), 67. |
| [17] | Goosse, H., Barriat, P., Lefebvre, W., Loutre, M., & Zunz, V. (2010). Introduction to climate dynamics and climate modeling. Online textbook. In. |
| [25] | Radojević, N., Kostadinović, D., Vlajković, H., & Veg, E. (2014). Microclimate control in greenhouses. FME Transactions, 42(2), 167-171. |
| [31] | Villarreal-Guerrero, F., Kacira, M., Fitz-Rodríguez, E., Linker, R., Kubota, C., Giacomelli, G. A., & Arbel, A. (2012). Simulated performance of a greenhouse cooling control strategy with natural ventilation and fog cooling. Biosystems Engineering, 111(2), 217-228. |
[11, 14, 17, 25, 31]
. Natural ventilation depends upon normal air movement created by wind pressures or by gradients induced by differences in air temperature between the growing area and the outside environment. Mechanical ventilation is defined as air movement created by fans that bring air into the growing area through controllable openings built into the greenhouse walls and exhaust it through the fan assembly. The ability to change the size of inlets is important for proper design of mechanical ventilation systems. Fan ventilation is normally controlled by thermostats and in some cases by humidity sensing devices when relative humidity is the control parameter
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [8] | Chao, J., Knickerbocker, R., North, P., Swift, D., Long, A., & Shtylla, B. (2014). Simple Model of Temperature in the Pomona College Organic Farm Greenhouse. |
| [11] | Dwyer, D. (2014). Defining ventilation boundary conditions for a greenhouse climate model. |
| [31] | Villarreal-Guerrero, F., Kacira, M., Fitz-Rodríguez, E., Linker, R., Kubota, C., Giacomelli, G. A., & Arbel, A. (2012). Simulated performance of a greenhouse cooling control strategy with natural ventilation and fog cooling. Biosystems Engineering, 111(2), 217-228. |
[7, 8, 11, 31]
.
There are two primary reasons airflow is necessary in greenhouses: to remove excess heat through ventilation as the temperature rises, replacing hot air with cooler air, and to control relative humidity and carbon dioxide within the plant canopy. A single system can serve both needs in smaller greenhouses, while separate exhaust and circulation systems are common in larger-sized greenhouses. Separate systems need to be carefully coordinated and adjusted to work together instead of counteracting each other Air movement systems range from simple, do-it-yourself arrangements to professionally designed, installed and integrated computer controlled systems
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [8] | Chao, J., Knickerbocker, R., North, P., Swift, D., Long, A., & Shtylla, B. (2014). Simple Model of Temperature in the Pomona College Organic Farm Greenhouse. |
| [11] | Dwyer, D. (2014). Defining ventilation boundary conditions for a greenhouse climate model. |
| [31] | Villarreal-Guerrero, F., Kacira, M., Fitz-Rodríguez, E., Linker, R., Kubota, C., Giacomelli, G. A., & Arbel, A. (2012). Simulated performance of a greenhouse cooling control strategy with natural ventilation and fog cooling. Biosystems Engineering, 111(2), 217-228. |
[7, 8, 11, 31].
3. Materials and Methods
3.1. Introduction
To promote good growth of plants, greenhouses, require either heating or cooling depending with the climatic conditions of the region they are, but equally important they require ventilation during hot days. In relation to CHMT inside a greenhouse, this is required for two reasons: to regulate the internal temperature and to remove water vapor transpired by the plants which are done through ventilation, caused by pressure differences or natural buoyancy forces through ventilators located either on top, on the sides, or both. Air movement and mixing within the greenhouse has a direct influence on the energy exchange of the vegetation. Therefore, it is important that the ventilators are designed correctly and the rate of ventilation controlled adequately. Cultivation technologies are developing with time aiming to lower the cost of production as they gain widespread acceptance and this drives the needs for a knowledge-rich information technology as we move from the information age to a knowledge-driven society. This have increased the efforts based on modern communication technologies to provide the missing bridge from the expert teams or knowledge bases to the low-level controllers of the production side
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [11] | Dwyer, D. (2014). Defining ventilation boundary conditions for a greenhouse climate model. |
| [14] | Fahmy, F. H., Farghally, H. M., Ahmed, N. M., & Nafeh, A. (2012). Modeling and simulation of evaporative cooling system in controlled environment greenhouse. Smart Grid and Renewable Energy, 3(01), 67. |
| [23] | Potdar, S. R., Patil, C. B., & Mudholkar, R. R. Greenhouse Air-Temperature Modelling and Fuzzy Logic Control. |
| [25] | Radojević, N., Kostadinović, D., Vlajković, H., & Veg, E. (2014). Microclimate control in greenhouses. FME Transactions, 42(2), 167-171. |
[7, 11, 14, 23, 25]
.
In this thesis, the understanding of transport mechanisms leading to the estimation of energy and mass balances of the greenhouse system was very important. The study involved the solar radiation, exchange by convection between the plants, structural parts and the internal and external air, latent heat produced by condensation and vaporization of the water inside and the exchange through evapo-transpiration process of the plants inside. The processes of thermal energy exchange among the greenhouse, the surroundings, and the greenhouse components are illustrated in
Figure 6 | [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [23] | Potdar, S. R., Patil, C. B., & Mudholkar, R. R. Greenhouse Air-Temperature Modelling and Fuzzy Logic Control. |
| [25] | Radojević, N., Kostadinović, D., Vlajković, H., & Veg, E. (2014). Microclimate control in greenhouses. FME Transactions, 42(2), 167-171. |
| [28] | Roy, J., Boulard, T., Kittas, C., & Wang, S. (2002). PA—Precision Agriculture: convective and ventilation transfers in greenhouses, Part 1: the greenhouse considered as a perfectly stirred tank. Biosystems Engineering, 83(1), 1-20. |
[10, 23, 25, 28]
.
3.2. Modes of CHMT for Gases and Vapor Inside the Greenhouse
3.2.1. Introduction
The dynamic behaviour of the micro-climate inside greenhouses is a combination of physical processes involving energy transfer and water vapour fluxes. These processes depend on the outside environmental conditions, structure of the greenhouse, type and state of the crop and on the effect of the control actuators
| [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
[5-7, 10]
. For successful growing of plants inside greenhouses, climate variables mainly temperature and humidity need to be studied carefully. These environmental factors are not possible to change but their effects can be altered. The idea behind greenhouses farming is to alter these environmental factors of a small enclosed region to favor growth of plants that can otherwise not be grown in the original state of these factors. The
Table 1 shows some plants and the environmental factors that favors their optimum yields.
Table 1. Plants and the environmental factors that favor their optimum yields.
Plant | Temperature range | Relative humidity range |
Tomato | 17 – 22°C | 65 - 75% |
Kale | 17 – 22°C | 70 - 80% |
Cabbage | 15 - 20°C | 70 - 80% |
Strawberries | 15 - 23°C | 64 - 77% |
Grapes | 15 - 30˚C | 60 - 70% |
Peas | 12 - 24 °C | 70 - 80% |
3.2.2. Temperature
Air temperature influences the energy balance of the plant canopy through the convective heat transfer to the plant leaves and bodies and this affect air movement in the greenhouse. The optimal level of the air temperature in the greenhouse depends on the photosynthetical activity of the plant in question, under the influence of the intensity of solar radiation on disposal, that is, for each light intensity, there is an optimal air temperature, enabling maximum photosynthetical activity
| [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [25] | Radojević, N., Kostadinović, D., Vlajković, H., & Veg, E. (2014). Microclimate control in greenhouses. FME Transactions, 42(2), 167-171. |
[5-7, 10, 24, 25]
.
3.2.3. Humidity
Water transport between the plant canopy and the environment is one of the most important parameters of the photosynthetical activity. The water vapour transport depends mainly on light intensity at disposal, temperature of the environment, and root characteristics of the plant in question in combination with the ability of the cultivation base to offer the necessary water quantity, but also on the air humidity of the plant environment. The air humidity influences the greenhouse climate characteristics and transpiration of the plant leaves. The intensity of the water transport of the plants depends directly on the temperature inside the greenhouse,
Figure 8 | [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [25] | Radojević, N., Kostadinović, D., Vlajković, H., & Veg, E. (2014). Microclimate control in greenhouses. FME Transactions, 42(2), 167-171. |
[5-7, 10, 24, 25]
.
3.3. The Dynamic MATLAB/SIMULINK Auto-tuned PID Controlled Model
3.3.1. Introduction
As internal air diffuses from one point to another inside the greenhouse, it moves with the energy it possess resulting to heat flow rate. These movements of particles with the energy they possess constitute the CHMT. The
Figures 7 and 8 show the convective heat and mass flow of a mixture of components making the greenhouse air, while
figure 1 represent a diagrammatic view of the sample greenhouse under study
| [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [6] | Bergman, T. L., & Incropera, F. P. (2011). Fundamentals of heat and mass transfer: John Wiley & Sons. |
| [7] | Boulard, T., & Wang, S. (2000). Greenhouse crop transpiration simulation from external climate conditions. Agricultural and forest meteorology, 100(1), 25-34. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[5-7, 10, 24, 27]
.
3.3.2. Heat Transfer Equation
The amount of heat balance in the greenhouse is a multidimensional quantity consisting of heat transfer and mass exchange to and from the greenhouse environment. The parameters involved in the physical process of the greenhouse are in an energy balance with the environment and, all together, are in an energy balance with the greenhouse environment. The heat balance according to
Figure 6 was expressed by equation (
1) as developed by
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[10, 24, 27]
.
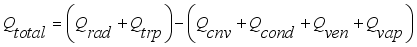 (1)
(1) Where each heat in Js
-1 sub-model
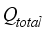
is net heat flux supplied into the greenhouse,
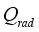
is heat flux supplied from solar radiation,
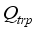
is heat flux of transpiration,
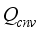
is heat flux exchanged between interior air and greenhouse cover,
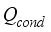
is heat flux supplied by condensation,
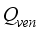
is heat flux exchanged through the ventilation and
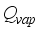
is heat flux exchanged through the ventilation; are defined by
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
[10]
as,
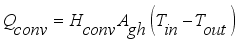
;
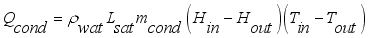
;
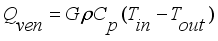
;
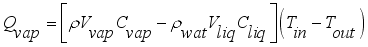
and
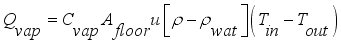
.
Figure 6. Heat transfer fluxes with the internal air in a greenhouse.
The convection heat transfer model for greenhouse was represented by an air temperature sub-model of the internal air as the parameters of the convection process between the cover, the greenhouse air and the floor. The internal temperature for the model was thus calculated using equation (
2) developed by
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[10, 24, 27]
:
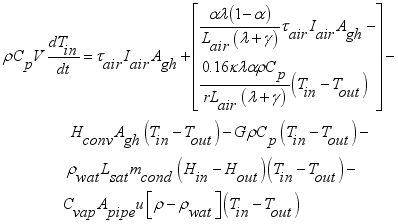 (2)
(2) Rearranging the terms of equation (
2) in favor of
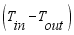
,
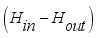
,
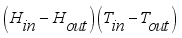
and the constant term, the equation yielded (
3) below.
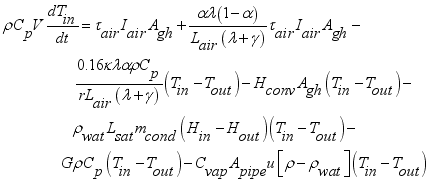 (3)
(3) Which further simplified to,
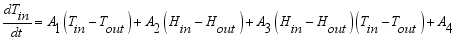 (4)
(4) 3.3.3. Mass Transfer Equation
Convective mass balance for the internal relative humidity a given ventilation rate and a rate of moisture production for the considered greenhouse was performed. As
Figure 7 shows the main sources of vapor in a greenhouse are crop transpiration, evaporation of the soil surface and pools, and water influx by fogging or cooling
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[10, 24, 27].
Figure 7. Mass transfer fluxes with the internal air in a greenhouse.
The model describing the changes in the water vapor content of the air inside the greenhouse is based on the mass balance equation, equation (
5) below as used by
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[10, 24, 27]
:
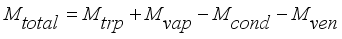 (5)
(5) Where each mass in kgm
-2s
-1 sub-model,
is net mass flux content of inside the greenhouse,
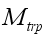
is mass flux due to transpiration process,
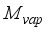
is mass flux of water vapour from irrigated water,
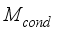
is mass flux due to condensation process and
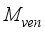
is mass lost flux due to ventilation; are defined by the equations,
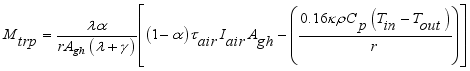
;
The total mass of gases inside the greenhouse was given by the differential equation (
6) assuming that there is no mass lost in the process.
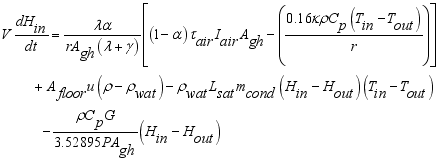 (6)
(6) Like equation (
2), rearranging the terms of (
6) in favor of
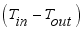
,
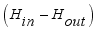
,
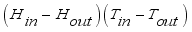
and the constant term, the equation was written as equations (
7) below.
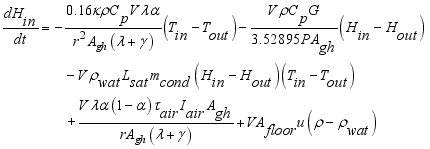 (7)
(7) Which was further written as,
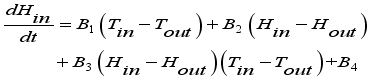 (8)
(8) 3.4. The Dynamic MATLAB/SIMULINK model
3.4.1. Introduction
As shown in equations (
4) and (
8), the mathematical model for the air inside a greenhouse includes two nonlinear differential equations, which are related to each other so much, with a complex relationship between the variables making direct calculation difficult. In this research, the dynamic model was designed by a SIMULINK blocks diagram using SIMULINK toolbox in MATLAB.
3.4.2. Greenhouse Model
The climate produced in a greenhouse is the result of complex mechanisms involving the processes of heat and mass exchange. The internal climate is also strongly dependent on the outside conditions, especially in unheated greenhouses. In greenhouse climate models the parameters of the internal climate such as air, soil and crop temperatures, and air humidity are calculated using energy and water vapor balances for the various components of the system. The dynamic behavior of the microclimate inside a greenhouse is a combination of physical systems involving internal heat transfer and mass balance. The HMT coefficients are functions of the system variables and it is important that they are formulated under relevant conditions of the greenhouse situation
| [9] | Chaturvedi, D. K. (2009). Modeling and simulation of systems using MATLAB and Simulink: CRC Press. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [24] | Raczek, A., & Wachowicz, E. (2014). Heat and mass exchange model in the air inside a greenhouse. Agricultural Engineering, 149, 185-195. |
| [27] | Rodríguez, F., Yebra, L., Berenguel, M., & Dormido, S. (2002). Modelling and simulation of greenhouse climate using Dymola. Paper presented at the IFAC 15th Triennial World Congress. Barcelona. Pp. |
[9, 10, 24, 27]
. Further, greenhouse climate models are specific for a greenhouse type, crop, region and weather conditions and the models are formulated and validated for those specific conditions and it is not possible to directly extrapolate them to different conditions, since they may produce erroneous predictions; thus the need for a model to be formulated for the current geographical location, the Central Kenya region, shown by the pair of equations (
9).
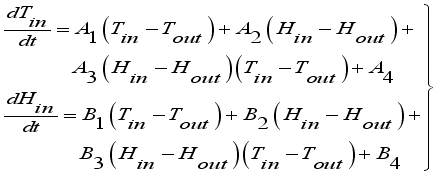 (9)
(9) Where
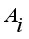
and
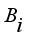
for
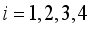
are the air climate parameters inside the greenhouse defined in Appendix.
3.4.3. SIMULINK Model Implementation
SIMULINK is a software package based in MATLAB which is used for modeling, analyzing, and simulating a wide variety of dynamic systems. SIMULINK provides a graphical interface for constructing the models. It is particularly useful for studying the effect of nonlinearities on the behavior of the system. The designed CHMT model composed of two main differential equations, (4) and (8) related to the greenhouse temperature and humidity of internal air. Therefore, this model was divided into temperature and humidity sub-models as in
Figure 8 for the internal air. During the modeling process, it was possible to add new customized blocks. The initialization of the model was performed by a designed MATLAB program that loads in the workspace of MATLAB the greenhouse structure data, the characteristic of the materials used in the greenhouse, the features of the actuator systems, universal physical constants, values of the coefficients involved in the physical processes, crop data, and the initial values of state, output, characteristic, and disturbance variables as shown by flow diagram
Figure 8. Further, SIMULINK reads the values of the available external variables contained in data files
| [3] | Ali, R. B., Aridhi, E., & Mami, A. (2015). Dynamic model of an agricultural greenhouse using Matlab-Simulink environment. Paper presented at the Sciences and Techniques of Automatic Control and Computer Engineering (STA), 2015 16th International Conference on. |
| [9] | Chaturvedi, D. K. (2009). Modeling and simulation of systems using MATLAB and Simulink: CRC Press. |
| [20] | Karris, S. T. (2006). Introduction to Simulink with engineering applications: Orchard Publications. |
| [23] | Potdar, S. R., Patil, C. B., & Mudholkar, R. R. Greenhouse Air-Temperature Modelling and Fuzzy Logic Control. |
[3, 9, 20, 23].
On the other hand, the simulation of this model involved the solution of governing differential equations also done by SIMULINK solvers for such equations.
Figure 8. Simulink scheme for greenhouse model.
3.4.4. PID-Controller Theory
The greenhouse environment control problem was to create a favorable environment for the crop in order to reach predetermined results for high yield, high quality and low costs. It was difficult to implement control problem practically due to the complexity of the greenhouse environments; however, most of these approaches are either theoretically complex or difficult to implement in the actual greenhouse production, and in this problem the controller method adopted was PID-controller method due to its simple architecture, easy implementation and excellent performance. These terms, proportional, integral, and derivative are then summed to calculate the output of the PID controller as shown by equation (
10). PID controller, shown by
Figures 9 and 10, is a control loop feedback mechanism widely used to control systems. In this thesis, the controller attempts to minimize the difference between the measured and expected values shown by
Figure 9 by adjusting the greenhouse processes through the three PID parameters and then determining the weighted sum which was then adjusted by tuning. By tuning the three parameters in the PID controller algorithm, the controller can provide control action designed for specific process requirements as explained by
| [1] | Afou, Y., Belkoura, L., & Qutanoute, M. (2014). Feedback Techniques Using PID and PI-Intelligent For Greenhouse Temperature. International journal of advanced research in electrical, electronics and instrumentation engineering, 3(6), 9779-9792. |
| [2] | Alghannam, A. R. O. (2012). Using proportional integral derivative and Fuzzy logic with optimization for greenhouse. International Journal of Latest Trends in Agriculture and Food Sciences, 2(2). |
| [4] | Ang, K. H., Chong, G., & Li, Y. (2005). PID control system analysis, design, and technology. IEEE transactions on control systems technology, 13(4), 559-576. |
| [13] | El Afou, Y., Belkoura, L., Outanoute, M., Guerbaoui, M., Rahali, A., Ed-Dahhak, A.,... Bouchikhi, B. (2014). Feedback techniques using PID and PI-intelligent for greenhouse temperature control. International journal of advanced research in electrical, electronics and instrumentation engineering, 3(6), 9779-9792. |
| [22] | O'Dwyer, A. (2009). Handbook of PI and PID controller tuning rules: Imperial College Press. |
[1, 2, 4, 13, 22]
.
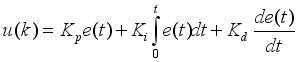 (10)
(10) Where,
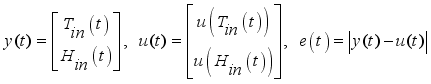 (11)
(11) PID tuning is the process of finding the values of proportional, integral, and derivative gains of a PID controller to achieve desired performance and meet design requirements. Traditionally, PID controllers are tuned either manually or using rule-based methods. Manual tuning methods are iterative and time-consuming, and if used on hardware, they can cause damage
| [1] | Afou, Y., Belkoura, L., & Qutanoute, M. (2014). Feedback Techniques Using PID and PI-Intelligent For Greenhouse Temperature. International journal of advanced research in electrical, electronics and instrumentation engineering, 3(6), 9779-9792. |
| [2] | Alghannam, A. R. O. (2012). Using proportional integral derivative and Fuzzy logic with optimization for greenhouse. International Journal of Latest Trends in Agriculture and Food Sciences, 2(2). |
| [4] | Ang, K. H., Chong, G., & Li, Y. (2005). PID control system analysis, design, and technology. IEEE transactions on control systems technology, 13(4), 559-576. |
| [13] | El Afou, Y., Belkoura, L., Outanoute, M., Guerbaoui, M., Rahali, A., Ed-Dahhak, A.,... Bouchikhi, B. (2014). Feedback techniques using PID and PI-intelligent for greenhouse temperature control. International journal of advanced research in electrical, electronics and instrumentation engineering, 3(6), 9779-9792. |
| [22] | O'Dwyer, A. (2009). Handbook of PI and PID controller tuning rules: Imperial College Press. |
[1, 2, 4, 13, 22]
. In this research, PID controllers were automatically tuned to achieve the optimal system design and to meet design requirements, since plant modeled could not be handled using traditional rule-based methods accurately,
Figure 9. This automated PID tuning workflow involved:
1. Identifying greenhouse model from input-output test data,
2. Modeling PID controllers in Simulink using PID Controller blocks,
3. Automatically tuning PID controller gains and fine-tune your design interactively,
4. Tuning multiple controllers in batch mode, and,
5. Tuning single-input single-output PID controllers as well as multi-loop PID controller architectures.
Figure 9. Block diagram of general PID controller.
Figure 10. PID-controller for Temperature and Humidity.
Note that the greenhouse dynamic system mentioned above is a two-input and two-output continuous time nonlinear system, as shown in
Figure 10. In order to simulate its behavior on a digital computer, the automatic PID-controller tuning was adopted to evaluate the PID terms as explained by Laplace transform of equation (
12) to get
| [1] | Afou, Y., Belkoura, L., & Qutanoute, M. (2014). Feedback Techniques Using PID and PI-Intelligent For Greenhouse Temperature. International journal of advanced research in electrical, electronics and instrumentation engineering, 3(6), 9779-9792. |
| [13] | El Afou, Y., Belkoura, L., Outanoute, M., Guerbaoui, M., Rahali, A., Ed-Dahhak, A.,... Bouchikhi, B. (2014). Feedback techniques using PID and PI-intelligent for greenhouse temperature control. International journal of advanced research in electrical, electronics and instrumentation engineering, 3(6), 9779-9792. |
| [22] | O'Dwyer, A. (2009). Handbook of PI and PID controller tuning rules: Imperial College Press. |
[1, 13, 22]
.
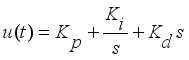 (12)
(12) The performance of the PID controller mainly depends on the selection of the PID parameters as shown by the table below:
Table 2. Effects of Kp, Ki and Kd tuning.
Losed-loop response | Rise time | Settling time | Overshoot | Steady-state error | Stability |
Increasing Kp | Decrease | Increase | Small increase | Decrease | Degrade |
Increasing Ki | Small decrease | Increase | Increase | Large decrease | Degrade |
Increasing Kd | Small decrease | Decrease | Decrease | Minor change | Improve |
3.5. Validation and Verification of the Results
In this part, the simulation results of the MATLAB-SIMULINK and RKM4 solutions models were compared against a set of analytical solutions of equations (
9) for some selected crops that were proposed to be grown in the modeled greenhouse. The validation process was performed on the developed models for some crops to be grown in the greenhouse based on individual crop demand in
Table 1 before adoption. The validation process was used to demonstrate that the model produced reasonable representation of the actual system and that it reproduces system behaviour with enough fidelity to satisfy analysis objectives while verification is the process that ensures the conceptual model is reflected accurately in the computerized representation. There are several methods used in validating and verifying a model and to guarantee that the model predicts accurately the reality for which it was built. The validation was based on the convergence of RKM4 solutions for some crops given by
Table 1 | [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
[10]
. For most models there are three separate aspects which should be considered during model validation and verification:
1. Assumptions
2. Input parameter values and distributions
3. Output values and conclusions.
4. Results and Discussion
4.1. Introduction
The solution of the temperatures inside the greenhouse was based on decreasing the energy inputs and eliminating their excesses; in cases where heating is used, the artificial energy input is eliminated by turning it off while to decrease natural inputs, solar radiation was minimized by means of shading, inside or outside the greenhouse. The increase in energy losses was achieved by ventilation. Every ventilation system was used to regulate the interior air temperature by diffusion to the outside air due to their temperature gradients and this diffusion in tern affected humidity. If the interior temperature must be further decreased, active cooling methods are usually applied. Ventilation is the air exchange between the greenhouse and the exterior through the greenhouse openings, vents and slits. The air renewal allows the evacuation of the excess heat and a decrease in the air temperature, modifying the atmospheric humidity, and modifying the gas composition of the atmosphere. If the air leaving the greenhouse is dry, the energy evacuated is very limited due to the low specific heat of dry air, while if it’s humid, the temperature decrease will be much higher, as the energy evacuated with the humid greenhouse air is much bigger. Therefore, the humidity difference between the interior and exterior is more important than the temperature difference, for greenhouse cooling purposes
| [5] | Bartzanas, T., & Kittas, C. (2004). Heat and mass transfer in a large evaporative cooled greenhouse equipped with a progressive shading. Paper presented at the International Conference on Sustainable Greenhouse Systems-Greensys 2004 691. |
| [8] | Chao, J., Knickerbocker, R., North, P., Swift, D., Long, A., & Shtylla, B. (2014). Simple Model of Temperature in the Pomona College Organic Farm Greenhouse. |
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
| [25] | Radojević, N., Kostadinović, D., Vlajković, H., & Veg, E. (2014). Microclimate control in greenhouses. FME Transactions, 42(2), 167-171. |
[5, 8, 10, 25]
.
4.2. The Dynamic MATLAB/SIMULINK Auto-tuned PID Controlled Model
4.2.1. Introduction
The system of differential equations (
9) representing the greenhouse temperature and humidity of internal air were first modelled as separate sub-models using SIMULINK then the sub-models were then joined together via the common parameters. This part describe how the sub-models were created and then represent them by block SIMULINK diagrams. The part concludes by combining the sub-models with PID controllers and perform an auto-tuning of the controllers.
4.2.2. Dynamic MATLAB/SIMULINK
Dynamic mathematical model of the microclimate inside the greenhouse comprised of energy and mass balance equations and the functions of each mode of transfer that affect convectional flow of air and gases. In the study, four components of heat transfer sub-model and three components of mass transfer sub-model
| [17] | Goosse, H., Barriat, P., Lefebvre, W., Loutre, M., & Zunz, V. (2010). Introduction to climate dynamics and climate modeling. Online textbook. In. |
| [25] | Radojević, N., Kostadinović, D., Vlajković, H., & Veg, E. (2014). Microclimate control in greenhouses. FME Transactions, 42(2), 167-171. |
[17, 25]
. In each of the two sub-models, each component comprised of a subsystem SIMULINK bock with the inputs and outputs described by the respective equation. Lastly, basing the SIMULINK model on three inputs, the humidity and temperature of the environment where the greenhouse is to be built, and the area available, a mathematical sub-models represented by
Figures 11 and 12 below were developed for the internal temperature and humidity, respectively, of the greenhouses for the region under study based on the outside conditions and the expected conditions for the target crop, as shown by Appendix IV. Two temperature-humidity recorders were adopted to measure the air temperature and relative humidity both inside and outside the greenhouse
| [3] | Ali, R. B., Aridhi, E., & Mami, A. (2015). Dynamic model of an agricultural greenhouse using Matlab-Simulink environment. Paper presented at the Sciences and Techniques of Automatic Control and Computer Engineering (STA), 2015 16th International Conference on. |
| [9] | Chaturvedi, D. K. (2009). Modeling and simulation of systems using MATLAB and Simulink: CRC Press. |
| [20] | Karris, S. T. (2006). Introduction to Simulink with engineering applications: Orchard Publications. |
| [23] | Potdar, S. R., Patil, C. B., & Mudholkar, R. R. Greenhouse Air-Temperature Modelling and Fuzzy Logic Control. |
[3, 9, 20, 23].
Figure 11. SIMULINK block for the internal temperature model in the greenhouse under study.
Figure 12. SIMULINK block for the internal humidity model in the greenhouse under study.
4.2.3. Analysis of the PID-Controlled Model
In this Chapter, simulating tests were carried out to evaluate the proposed PID controller for internal temperature and humidity controllers. On
Figures 11 and 12, the PID controller, on
Figure 10 was incorporated to produce the controlled greenhouse
Figure 11 which using SIMULINK blocks was represented as
Figure 13 below. The appropriate tuning was done to produce the required simulated temperature and humidity subject to requirements of Appendix IV taking care of both over-shoot and under-shoot of temperature and humidity which could have adverse negative effects on production of the plants being grown. This show the need to adopt automatically controlled ventilation systems as this could reduce the extent of the over-shoot and/or the under-shoot. Lastly, the potential of the designed controllers for internal greenhouse environment quality control was discussed based on the simulating results.
Figure 13. Dynamic Model of the CHMT using MATLAB-SIMULINK for Ventilation and Cooling Systems inside a Greenhouse.
After running the MATLAB-SIMULINK model in
figure 13, the results got were graphically represented by
figures 14 and 15 and further by
table 3 for simulated internal temperature and internal humidity respectively, and proved the proposed automatic PID controller has excellent performance on efficient auto tuning of the parameters only when needed; fast response speed; small overshot; small steady error; and stability and adaptability response to uncertain factors. These advantages make the proposed controller suitable for solving the major difficulties in internal micro-climate control.
In determining the model solution, the range of temperature and humidity used were based on optimal values of the plants conditions represented by
table 1.
Figure 15. Graphical representation of the Simulated Temperature.
Figure 15. Graphical representation of the Simulated Humidity.
4.3. Validation and Verification of the Results
Lastly, an extensive comparison was done between the climatical requirements of some selected crops to be grown in the greenhouses, the numerically calculated internal temperature and humidity and the PID-controlled simulated internal temperature distribution and humidity for the greenhouse and represented by
table 3 below. This showed the high level of accuracy of the PID-controlled model based on the theoretical values got for a similar numerical model by
| [10] | Dickson Kande, Titus Rotich, Fredrick Nyamwala. (2023). Numerical Model for the Convective Heat and Mass Flow for the Internal Climate of Greenhouse. International Journal of Systems Science and Applied Mathematics, 8(3), 31-44. |
[10].
Table 3. Comparison of the numerically calculated and the PID-controlled internal conditions for the crops targeted to be planted in the modelled greenhouse.
Tout °C | Hout in % | Average required Temp | Average required Hum | Model Calculated Tin in °C | Model Calculated Hin in % | PID-Controlled Temp in °C | Error / Absolute Difference | PID-Controlled Hum in % | Error / Absolute Difference |
15 | 54 | 19.5 | 70 | 15.0004779 | 53.9999439 | 15.000273 | 0.00020495 | 54.00081681 | 0.00087295 |
16 | 56 | 19.5 | 75 | 16.0004609 | 55.9999474 | 16.0003797 | 0.0000817 | 56.00011592 | 0.00016855 |
17 | 59 | 17.5 | 70 | 17.0004375 | 58.9999505 | 17.000269 | 0.00016849 | 59.00124479 | 0.00129432 |
18 | 61 | 19 | 70.5 | 18.0004232 | 60.9999532 | 18.0002679 | 0.00015524 | 60.00005041 | 0.99990281 |
19 | 62 | 22.5 | 65 | 19.0004163 | 61.9999557 | 19.0002532 | 0.00016315 | 62.00117692 | 0.00122124 |
20 | 65 | 18 | 75 | 20.0003972 | 64.9999579 | 20.0027114 | 0.00231427 | 65.00012291 | 0.00016500 |
21 | 67 | 17.5 | 70 | 21.0003853 | 66.9999599 | 21.0002908 | 0.0000945 | 67.00023604 | 0.00027613 |
22 | 70 | 22.5 | 65 | 22.0003688 | 69.9999617 | 22.0003703 | 0.00000145 | 70.00117578 | 0.00121405 |
23 | 74 | 17.5 | 70 | 23.0003489 | 73.9999634 | 23.0027195 | 0.00237061 | 74.00114264 | 0.00117925 |
24 | 77 | 18.0 | 75 | 24.0003353 | 76.9999649 | 24.0000846 | 0.00025071 | 77.00014537 | 0.00018045 |
25 | 79 | 19.5 | 75 | 25.0003269 | 78.9999663 | 25.0003571 | 0.00003028 | 79.00110091 | 0.00113459 |
26 | 80 | 17.5 | 70 | 26.0003228 | 79.9999676 | 26.0002924 | 0.00003039 | 80.00031915 | 0.00035153 |
27 | 80 | 19.0 | 70.5 | 27.0003228 | 79.9999688 | 27.0011917 | 0.0008689 | 81.00141423 | 1.00144541 |
28 | 81 | 18.0 | 75 | 28.0003188 | 80.9999699 | 28.0004938 | 0.00017504 | 83.00086801 | 2.00089808 |
29 | 81 | 22.5 | 65 | 29.0003188 | 80.9999710 | 29.0002757 | 4.3062E-05 | 85.00270399 | 4.00273302 |
30 | 81 | 22.5 | 65 | 30.0003188 | 80.9999719 | 30.0016826 | 0.00136385 | 88.00011952 | 7.00014759 |
Nomenclature
Iair= Solar radiation density, Wm2
Agh= Area of the cover of the greenhouse, m2
Cp= Specific heat of air inside the greenhouse, Jkg-1K-1
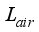
= Latent heat of vaporization, Jkg
-1 Tin = Air temperature inside the greenhouse, K
Tout = Air temperature outside the greenhouse, K
r= Radiative resistance
K= Unit conversion
Hconv= Heat transfer coefficient of the internal air between the floor and the cover, Wm-2K-1
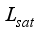
= Latent heat of saturation water, Jkg
-1 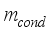
= Mass heat transfer coefficient at the surface of the greenhouse, ms
-1 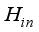
= Humidity of the air inside the greenhouse, %
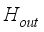
= External air humidity, %
G= Indoor and outdoor ventilation rate, m3s-1
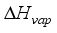
= Enthalpy of the water vapuor, Js
-1 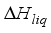
= Enthalpy of liquid water, Js
-1 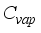 =
= Specific heat of water vapour inside the greenhouse, Jkg
-1K
-1 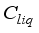 =
= Specific heat of water inside the greenhouse, Jkg
-1K
-1 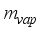
= Mass of vapour from the irrigated water, kgm
-2s
-1 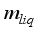
= Mass of the irrigated water, kgm
-2s
-1 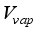
= Volume of water vapour inside greenhouse, m
3 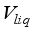
= Volume of irrigated water inside greenhouse volume, m
3 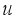
= Rate at which the irrigated water leaves the soil surface, ms
-1 V = Greenhouse volume, m3
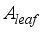
= Leaf area index for the greenhouse plants, m
2 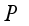
= Atmospheric pressure, Pa
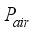
= Pressure of the air inside the greenhouse, Pa
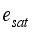
= Saturation vapor pressure, Pa
Rvap= Universal gas constant for water vapour, Jkg-1 K-1
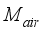
= Mass of air inside the greenhouse, kgm
-2s
-1 Rair= Universal gas constant for dry air, Jkg-1 K-1
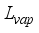
= Latent heat of vaporization, Jkg
-1 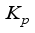 =
= Proportional gain for PID-controller
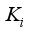 =
= Integral gain for PID-controller
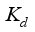
= Derivative gain for PID-controller
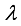 =
= Slope of saturation vapor pressure curve at air temperature, PaK
-1 α= Priestley-Taylor coefficient
ρ= Air density inside the greenhouse, kgm-3
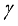
= Psychrometric constant, PaK
-1 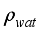
= Density of water, kgm
-3 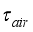
= Transmissivity of the greenhouse covering materials for solar radiation
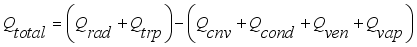 (1)
(1) 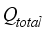 is net heat flux supplied into the greenhouse,
is net heat flux supplied into the greenhouse, 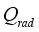 is heat flux supplied from solar radiation,
is heat flux supplied from solar radiation, 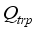 is heat flux of transpiration,
is heat flux of transpiration, 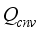 is heat flux exchanged between interior air and greenhouse cover,
is heat flux exchanged between interior air and greenhouse cover, 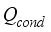 is heat flux supplied by condensation,
is heat flux supplied by condensation, 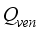 is heat flux exchanged through the ventilation and
is heat flux exchanged through the ventilation and 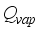 is heat flux exchanged through the ventilation; are defined by
is heat flux exchanged through the ventilation; are defined by 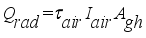
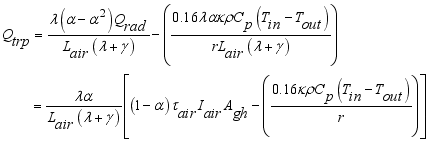
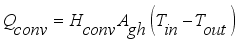 ;
; 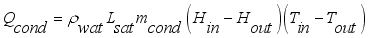 ;
; 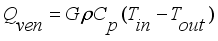 ;
; 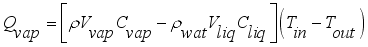 and
and 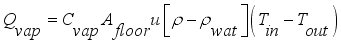 .
. 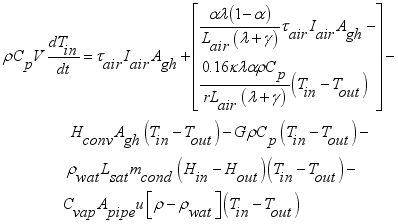 (2)
(2) 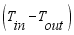 ,
, 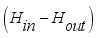 ,
, 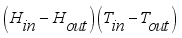 and the constant term, the equation yielded (3) below.
and the constant term, the equation yielded (3) below. 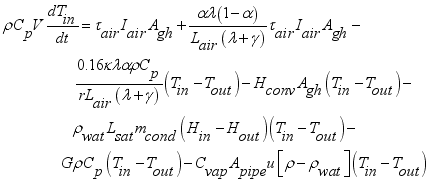 (3)
(3) 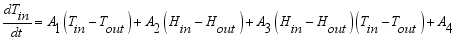 (4)
(4) 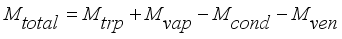 (5)
(5)  is net mass flux content of inside the greenhouse,
is net mass flux content of inside the greenhouse, 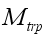 is mass flux due to transpiration process,
is mass flux due to transpiration process, 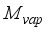 is mass flux of water vapour from irrigated water,
is mass flux of water vapour from irrigated water, 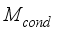 is mass flux due to condensation process and
is mass flux due to condensation process and 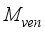 is mass lost flux due to ventilation; are defined by the equations,
is mass lost flux due to ventilation; are defined by the equations, 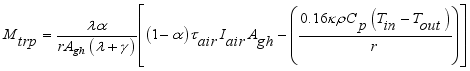 ;
; 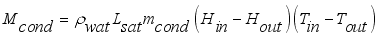
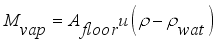 and
and 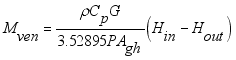 .
. 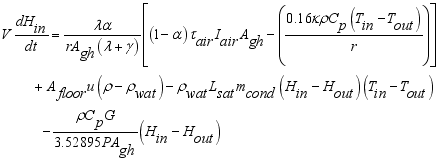 (6)
(6) 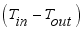 ,
, 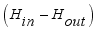 ,
, 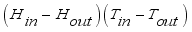 and the constant term, the equation was written as equations (7) below.
and the constant term, the equation was written as equations (7) below. 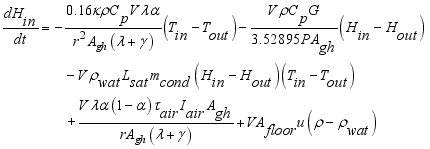 (7)
(7) 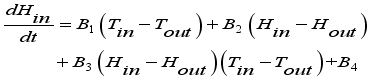 (8)
(8) 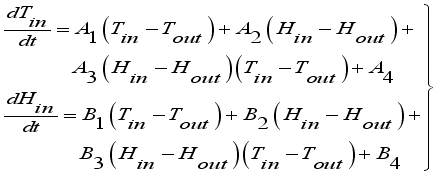 (9)
(9) 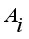 and
and 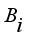 for
for 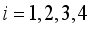 are the air climate parameters inside the greenhouse defined in Appendix.
are the air climate parameters inside the greenhouse defined in Appendix. 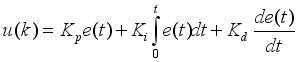 (10)
(10) 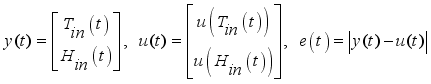 (11)
(11) 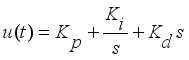 (12)
(12)  = Latent heat of vaporization, Jkg-1
= Latent heat of vaporization, Jkg-1  = Latent heat of saturation water, Jkg-1
= Latent heat of saturation water, Jkg-1  = Mass heat transfer coefficient at the surface of the greenhouse, ms-1
= Mass heat transfer coefficient at the surface of the greenhouse, ms-1 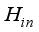 = Humidity of the air inside the greenhouse, %
= Humidity of the air inside the greenhouse, % 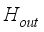 = External air humidity, %
= External air humidity, % 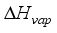 = Enthalpy of the water vapuor, Js-1
= Enthalpy of the water vapuor, Js-1 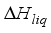 = Enthalpy of liquid water, Js-1
= Enthalpy of liquid water, Js-1 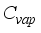 = Specific heat of water vapour inside the greenhouse, Jkg-1K-1
= Specific heat of water vapour inside the greenhouse, Jkg-1K-1 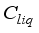 = Specific heat of water inside the greenhouse, Jkg-1K-1
= Specific heat of water inside the greenhouse, Jkg-1K-1 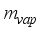 = Mass of vapour from the irrigated water, kgm-2s-1
= Mass of vapour from the irrigated water, kgm-2s-1 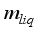 = Mass of the irrigated water, kgm-2s-1
= Mass of the irrigated water, kgm-2s-1 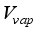 = Volume of water vapour inside greenhouse, m3
= Volume of water vapour inside greenhouse, m3 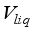 = Volume of irrigated water inside greenhouse volume, m3
= Volume of irrigated water inside greenhouse volume, m3 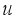 = Rate at which the irrigated water leaves the soil surface, ms-1
= Rate at which the irrigated water leaves the soil surface, ms-1 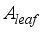 = Leaf area index for the greenhouse plants, m2
= Leaf area index for the greenhouse plants, m2 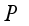 = Atmospheric pressure, Pa
= Atmospheric pressure, Pa 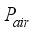 = Pressure of the air inside the greenhouse, Pa
= Pressure of the air inside the greenhouse, Pa 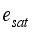 = Saturation vapor pressure, Pa
= Saturation vapor pressure, Pa 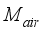 = Mass of air inside the greenhouse, kgm-2s-1
= Mass of air inside the greenhouse, kgm-2s-1 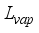 = Latent heat of vaporization, Jkg-1
= Latent heat of vaporization, Jkg-1 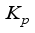 = Proportional gain for PID-controller
= Proportional gain for PID-controller 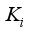 = Integral gain for PID-controller
= Integral gain for PID-controller 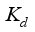 = Derivative gain for PID-controller
= Derivative gain for PID-controller 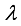 = Slope of saturation vapor pressure curve at air temperature, PaK-1
= Slope of saturation vapor pressure curve at air temperature, PaK-1 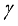 = Psychrometric constant, PaK-1
= Psychrometric constant, PaK-1 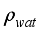 = Density of water, kgm-3
= Density of water, kgm-3 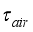 = Transmissivity of the greenhouse covering materials for solar radiation
= Transmissivity of the greenhouse covering materials for solar radiation